Python中树的相关操作！

树的存储、表示与遍历

树的存储与表示

顺序存储:将数据结构存储在固定的数组中,然在遍历速度上有一定的优势,但因所占空间比较大,是非主流二叉树。二叉树通常以链式存储。

某个节点为空是用0表示。

节点的结构：

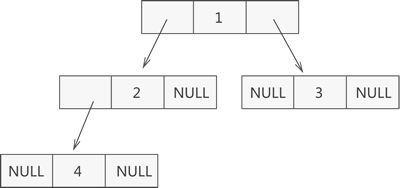
二叉树的建立

class Node(object):
    """二叉树节点的封装"""
    def __init__(self, element=None, lchild=None, rchild=None):
        self.element = element
        self.lchild = lchild
        self.rchild = rchild
class Tree(object):
    """二叉树的封装"""
    def __init__(self, root=None):
        self.root = root
    def __add__(self, element):
        # 插入节点的封装
        node = Node(element)
        # 1.判断是否为空，则对根结点进行赋值
        if not self.root:
            self.root = node
        # 2. 如果存在跟结点，将根结点放入队列
        else:
            queue = []
            # 将根结点放入队列中
            queue.append(self.root)
            # 对队列中的所有节点进行遍历
            # 这里的循环每次都是从根结点往下循环的
            while queue:
                # 3.弹出队列中的第一个元素(第一次弹出的为根节点，然后是根的左节点，根的右节点，依次类推)
                cur = queue.pop(0)
                if not cur.lchild:
                    cur.lchild = node
                    return
                elif not cur.rchild:
                    cur.rchild = node
                    return
                else:
                    # 左右子树都存在就将左右子树添加到队列中去
                    queue.append(cur.lchild)
                    queue.append(cur.rchild)

二叉树的遍历

遍历是指对树中所有结点的信息的访问,即依次对树中每个结点访问一次且仅访问一次,我们把这种对所有节点的访问称为遍历(traversal)

广度优先遍历（层次遍历）

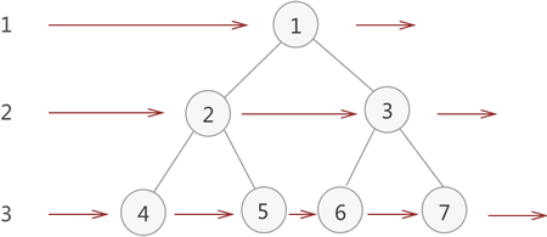
遍历结果为1，2，3，4，5，6，7

  def breadth_travel(self):
        """利用队列实现树的层次遍历"""
        if self.root == None:
            return
        # 将二叉树的节点依次放入队列中，通过访问队列的形式实现树的遍历
        queue = []
        queue.append(self.root)
        while queue:
            node = queue.pop(0)
            print(node.element, end=',')
            if node.lchild != None:
                queue.append(node.lchild)
            if node.rchild != None:
                queue.append(node.rchild)
        print()

深度优先遍历

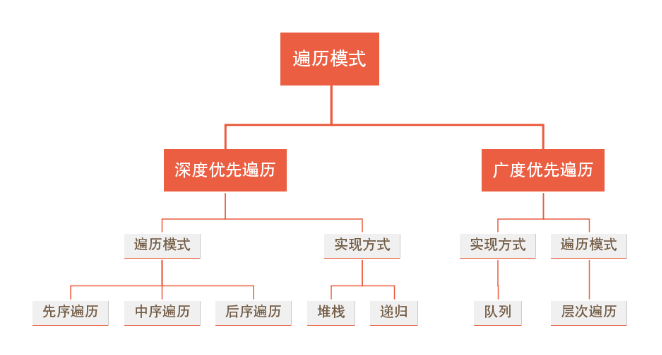
深度优先遍历有三种方式：

先序遍历（根->左->右）：先访问根结点，再先序遍历左子树，最后再先序遍历右子树，

中序遍历（左->根->右）：先中序遍历左子树，然后再访问根结点，最后再中序遍历右子树，

后序遍历（左->右->根）：先后序遍历左子树，然后再后序遍历右子树，最后再访问根结点。

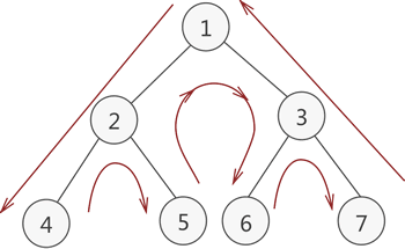
先序遍历： 1 2 4 5 3 6 7

中序遍历： 4 2 5 1 6 3 7

后序遍历： 4 5 2 6 7 3 1

递归实现先序遍历

# 深度优先遍历：先序遍历---根 左 右
    def preorder(self, root):
        """递归实现先序遍历"""
        if not root:
            return
        print(root.element, end=',')
        self.preorder(root.lchild)
        self.preorder(root.rchild)

递归实现中序遍历

# 深度优先遍历：中序遍历---左 根 右
    def inorder(self, root):
        """递归实现中序遍历"""
        if not root:
            return
        self.inorder(root.lchild)
        print(root.element, end=',')
        self.inorder(root.rchild)

递归实现后序遍历

    # 深度优先遍历：后序遍历---左 右 根
    def postorder(self, root):
        """递归实现后序遍历"""
        if not root:
            return
        self.postorder(root.lchild)
        self.postorder(root.rchild)
        print(root.element, end=',')

测试代码：

if __name__ == '__main__':
    binaryTree = Tree()
    for i in range(7):
        binaryTree.__add__(i+1)
    # 广度优先遍历
    print("广度优先：")
    binaryTree.breadth_travel()
    # 深度优先，先序遍历
    root = binaryTree.root
    binaryTree.preorder(root)
    print('深度优先--先序遍历')
    binaryTree.inorder(root)
    print('深度优先--中序遍历')
    binaryTree.postorder(root)
    print('深度优先--后序遍历')

广度优先：
1,2,3,4,5,6,7,
1,2,4,5,3,6,7,深度优先--先序遍历
4,2,5,1,6,3,7,深度优先--中序遍历
4,5,2,6,7,3,1,深度优先--后序遍历

和我们预期的结果完全相同。

想了解更多Python知识，请移步Python视频教程继续学习！！

内容版权声明：除非注明，否则皆为本站转载文章。文章及图片版权归原作者所有，如有侵权请联系我们，我们立刻删除。